ångstromCTF2021 was, in all honesty, probably the most serious I’ve been on a CTFTime CTF.

The spread of challenge difficulties was just right for a beginner like me. While I could not do any of the harder challenges (includes my nemesis, block ciphers), I was nonetheless able to solve quite a sizable number, including some I did not think possible.

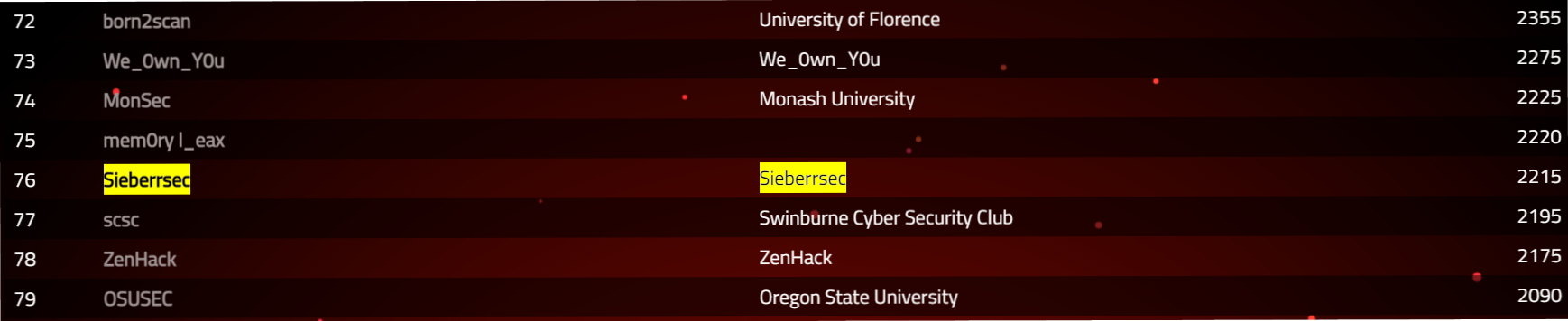
In the end, we reached 71st place in the CTF!

Writeups

I made writeups for the following two challenges (because I’m the most proud of them heh):

1. (Crypto) Subsitution
2. (Crypto) I’m So Random

Substitution

[Source](https://files.actf.co/3c66d046b7d644f65c4e4bbb0c7aa4c4420ef1b6fda684e1b00c261ccf6472be/chall.py)

nc crypto.2021.chall.actf.co 21601

Author: EvilMuffinHa

Reconnaissance

We are given the following code:

#!/usr/bin/python

from functools import reduce

with open("flag", "r") as f:
    key = [ord(x) for x in f.read().strip()]



def substitute(value):
    return (reduce(lambda x, y: x*value+y, key))%691



print("Enter a number and it will be returned with our super secret synthetic substitution technique")
while True:
    try:
        value = input("> ")
        if value == 'quit':
            quit()
        value = int(value)
        enc = substitute(value)
        print(">> ", end="")
        print(enc)
    except ValueError:
        print("Invalid input. ")

We can therefore make some observations:

1. If we recover the key, we recover the flag.
2. We need to understand how that substitute() function works. (because I didn’t before I saw this challenge)
3. Since 691 is a prime, we know that there is a bijective mapping between each input value and its substituted value.

Figuring out what substitute() does

Rewriting the code we get:

def substitute(value):
    return (reduce(lambda x, y: x*value+y, key))%691

def sub(value):
    c=key[0]
    for i in range(1,len(key)):
        c=(c*value+key[i])%691
    return c

And since the two functions give the same output for some dummy key, they are the same. (You can verify this by running it repeatedly.)

Thus we can see that the substitution algorithm is just, in math terms:

(Disclaimer: I lost my whiteboard workings so if this is incorrect please do notify me and I will give you a cookie 🍪.)

The Exploit

Notice that:

1. substitute() is just a glorified weighted checksum.
2. We can request for as many substitute()s as we desire.

It should be pretty obvious that we simply need to solve a series of n linear congruences to retrieve the flag.

This can be done by representing the linear congruences in a matrix and their results in a vector.

The only problem being that we don’t know how long the flag is…

So we will just BRUTEFORCE IT >:D.

The Script

Writing everything in SageMath,

from sage.all import *
from pwn import *

r=remote('crypto.2021.chall.actf.co', 21601)
def substitute(i):
    r.recvuntil('> ')
    r.sendline(str(i))
    return int(r.recvline()[3:])

R=Integers(691)
leest=[substitute(i) for i in range(5)]
for i in range(5,50):
    leest.append(substitute(i))
    A=Matrix(R,[[R(j)**R(k) for k in range(i+1)] for j in range(i+1)])
    v=vector(R,leest)
    sol=list(A.solve_right(v))
    print(''.join([chr(c) for c in sol][::-1]))
    # Sanity Check information unnecessary. Thus they were all removed.

We simply run the code to obtain the flag!

Flag: actf{polynomials_20a829322766642530cf69}

I’m So Random

Aplet's quirky and unique so he made my own [PRNG](https://files.actf.co/a155e414e8cc7e0279ffe40225d7295fda5c2b79116313c2cb8fb8bf22dda70d/chall.py)! It's not like the other PRNGs, its absolutely unbreakable!

nc crypto.2021.chall.actf.co 21600

Author: EvilMuffinHa

Reconnaissance

We are presented with the following code:

import time
import random
import os

class Generator():
    DIGITS = 8
    def __init__(self, seed):
        self.seed = seed
        assert(len(str(self.seed)) == self.DIGITS)

    def getNum(self):
        self.seed = int(str(self.seed**2).rjust(self.DIGITS*2, "0")[self.DIGITS//2:self.DIGITS + self.DIGITS//2])
        return self.seed


r1 = Generator(random.randint(10000000, 99999999))
r2 = Generator(random.randint(10000000, 99999999))


query_counter = 0
while True:
    query = input("Would you like to get a random output [r], or guess the next random number [g]? ")
    if query.lower() not in ["r", "g"]:
        print("Invalid input.")
        break
    else:
        if query.lower() == "r" and query_counter < 3:
            print(r1.getNum() * r2.getNum())
            query_counter += 1;
        elif query_counter >= 3 and query.lower() == "r":
            print("You don't get more random numbers!")
        else:
            for i in range(2):
                guess = int(input("What is your guess to the next value generated? "))
                if guess != r1.getNum() * r2.getNum():
                    print("Incorrect!")
                    exit()
            with open("flag", "r") as f:
                fleg = f.read()
            print("Congrats! Here's your flag: ")
            print(fleg)
            exit()

In brief, it creates a PRNG that generates numbers like so:

1. Generate 2 pseudo-randomly seeded PRNGs. (post-solve addendum: see middle-square method)

2. When each getNum() is called,

   a. Square the seed

   b. Pad the seed so it is 16 digits long.

   c. Extract the middle 8 digits of the seed.

   d. Return seed.

   e. Next getNum() will use this new seed.

3. Multiply the two PRNG-generated numbers to create a pseudo-random number (we will call this the Result).

That’s cool. But where’s the vulnerability?

The Exploit

Here >:D.

Notice that:

1. Result is pretty small (16 digits at best).

   a. Easily factorized.

2. The pseudo-randomly generated number is always the product of the two PRNG-generated numbers.

   a. So in the event that they are prime, factorizing the pseudoprime Result will leak both pseudo-random seeds.

3. For every pair of pseudo-random seeds, the PRNG-generated number is ALWAYS the same.

   a. That means that we can simply intercept the pseudo-random seeds and continue generating new Results as if nothing had happened.

This gives me an idea for an exploit:

1. Generate numbers repeatedly until we get a pseudoprime Result.

   a. This will happen with an \(\approx\) 1/64 chance.

   (A consequence of the Prime Number Theorem states that any integer n digits long has an \(\approx \frac{1}{ln(n)}\) chance of being prime. We have our PRNG-generated numbers being at most 8 digits.)

2. Factorize Result to intercept the seeds of the two PRNGs.
3. Create our own PRNGs with the two intercepted seeds and generate Results to get flag!

There’s really not much else to say, this solution was pretty simple in my eyes.

Script

# So here's the plan...
# We hope for a pseudoprime seed...
# And if we get it... we win! :D
from pwn import *
from sage.all import *

# context.log_level='DEBUG'

class Generator():
    DIGITS = 8
    def __init__(self, seed):
        self.seed = seed

    def getNum(self):
        self.seed = int(str(self.seed**2).rjust(self.DIGITS*2, "0")[self.DIGITS//2:self.DIGITS + self.DIGITS//2])
        return self.seed

const=24
j=0
while sum([i[1] for i in factor(const)])!=2:
    if not j%3:
        r=remote("crypto.2021.chall.actf.co",21600)
    r.recvuntil('? ')
    r.sendline('r')
    const=int(r.recvline()[:-1])
    j+=1
n1,n2=[i[0] for i in factor(const)]
print(f"Intercepted! n1: {n1} n2: {n2}")
r1 = Generator(n1)
r2 = Generator(n2)

r.recvuntil('? ')
r.sendline('g')
r.sendline(str(r1.getNum()*r2.getNum()))

r.recvuntil('? ')
r.sendline(str(r1.getNum()*r2.getNum()))

r.interactive()

And thus we run the exploit:

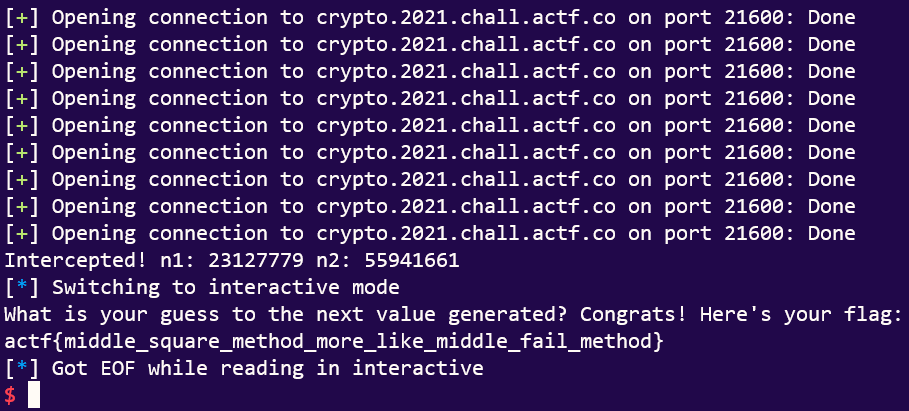
And receive our flag!

actf{middle_square_method_more_like_middle_fail_method}