Unfortunately I’m a little VERY MUCH short on time, let’s cut to the chase.
Writeups (WIP, might add more as time goes on)
Hopscotch
Keith wants to play hopscotch, but in order to make things interesting,
he decides to use a random number generator to decide the number of
squares n to draw for a round of hopscotch. He then creates a hopscotch
board on the floor by randomly creating a sequence of ones (one square)
and twos (two squares) such that the sum of all the numbers in the sequence
is n. Given 1 <= n <= 1000, find the number of valid hopscotch boards (mod 10000)
he can create.
Sample Input: 5
Sample Output: 8
nc hopscotch.hsc.tf 1337
Problem Analysis
Basically, find the number of sequences from ones and twos one can make that add up to \(n\).
This writeup is mainly a response to the other one on CTFTime.
While it is by no means bad (and you should go and rate the writer 5.0 for their work :O), I hope to share a more mathematical explanation for the problem solution.
Combinatorics: Recurrence Relations
Perhaps we should take the hopscotch board metaphor and extend it a bit further.
Basically, say we have a hopscotch board with a total of \(m\) squares, where \(m \in \mathbb{Z}\). Let \(F_m\) describe the number of ways one can make a hopscotch board with \(m\) squares in total.
(For illustration purposes, I have elected to use \(m=5\) and a badly-drawn hopscotch board.)

For a board with \(m+1\) squares total, we could just tack on another square at the back:
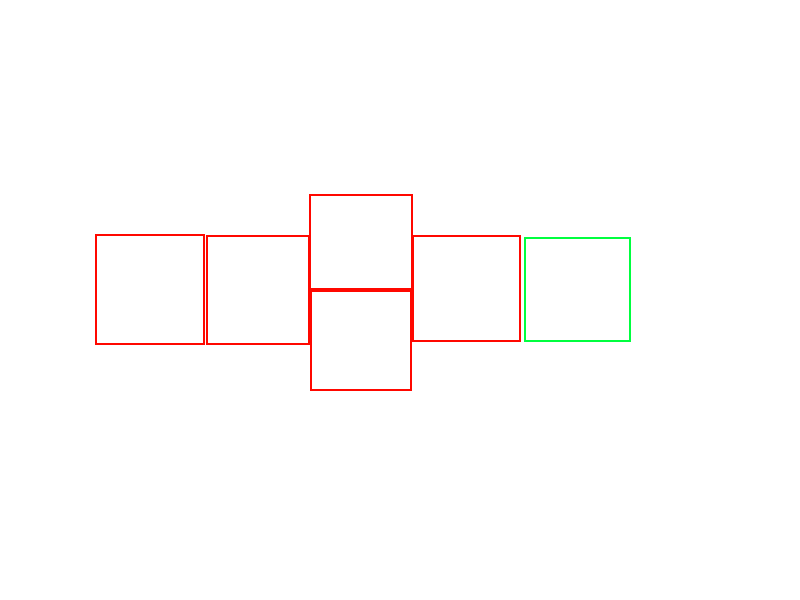
Similarly, for a board with \(m+2\) squares total, we could just tack on another two squares at the back:

Conversely, this also means for any hopscotch board with \(m\) squares, it could have been constructed from a hopscotch board from \(m-1\) (if it had 1 square at its right end) or \(m-2\) squares (if it had 2 squares at its right end).
Therefore, the total number of ways one can construct a hopscotch board with \(m\) squares is the same as the TOTAL number of ways that one can construct a hopscotch board with \(m-1\) squares and \(m-2\) squares.
Mathematically,
\[F_m=F_{m-1}+F_{m-2}\]Would you look at that. The Fibonacci sequence.
Solve Script
Taking what we have gathered from our combinatorial analysis, we can compute the number of sequences from **ones and twos** one can make that add up to n using a Fibonacci sequence.
from pwn import *
fibo=[1,1]
def precompute():
# Precomputation is faster, although frankly unnecessary.
while len(fibo)<=1000:
fibo.append((fibo[len(fibo)-1]+fibo[len(fibo)-2])%10000)
precompute()
r=remote('hopscotch.hsc.tf',1337)
r.recvuntil('\n')
try:
while True:
num=int(r.recvline()[:-1])
r.sendline(str(fibo[num]))
r.recvuntil(': ')
except Exception as e: # I'm lazy to detect the flag, so I'll just catch it...
print(e)
r.interactive()
And we’re done!
Flag: flag{wh4t_d0_y0U_w4nt_th3_fla5_t0_b3?_'wHaTeVeR_yOu_wAnT'}